数值流形方法（Numerical Manifold Method, NMM）是一个将连续-非连续物理问题统一在同一个数值框架中求解材料区域变形场的新颖模拟方法。该方法在计算小位移累积大变形、连续-非连续物理问题以及非连续面间位移阶跃和载荷传递等方面具有很高的精确度和适用性。实验室拓展了NMM程序框架，提出了流形单元开裂算法、界面粘聚力模型以及针对高聚物粘结炸药（Polymer Bonded Explosives, PBXs）细观各相的本构模型。通过提取炸药内部非均匀性特征，建立细观结构模型，开展了炸药变形和破坏的宏细观力学行为模拟。研究成果发表在Engineering Analysis with Boundary Elements，Journal of Energetic Materials和 Computational Materials Science等国际学术期刊上。

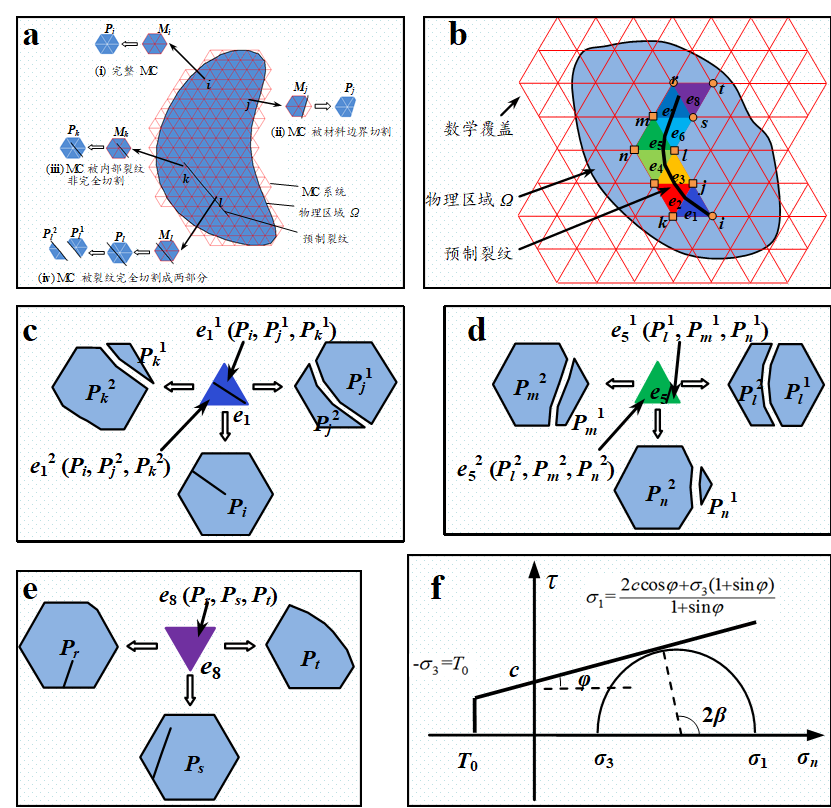
图1.  数值流形方法的基本概念 (a) 拓扑覆盖系统; (b) 流形单元定义; (c) 单元e1的构造; (d) 单元e5的构造; (e) 单元e8的构造; (f) 摩尔-库伦准则

 

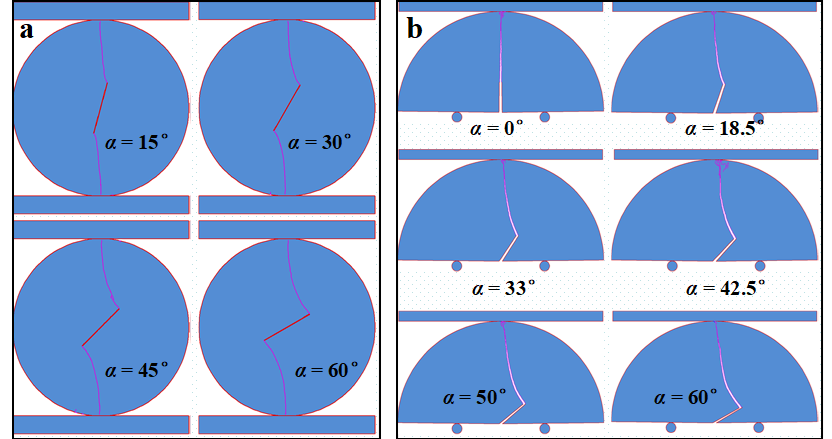
图2. 含预制斜裂纹材料的劈裂模拟 (a) 预制裂纹圆盘; (b) 预制裂纹半圆盘

 

图3.  炸药颗粒在刚性模具中压制破碎模拟 (a) 初始时刻力系传递; (b) 0.769 s时刻颗粒破碎状态; (c) 1-9号颗粒破碎情况; (d) 10-18号颗粒破碎情况; (e) 19-27号颗粒破碎情况

 

图4. PBX炸药细观模型及等效弹性模量模拟 (a) 炸药细观模型；(b) 炸药等效模量随炸药成分和体积分数的变化规律

 

图5. 含初始缺陷的炸药细观力学模拟 (a) 初始脱粘20%时拉伸破坏形貌以及不同脱粘系数下拉伸/压缩应力-应变曲线; (b) 裂纹密度4.0 mm-1时拉伸破坏形貌以及不同裂纹密度下拉伸/压缩应力-应变曲线